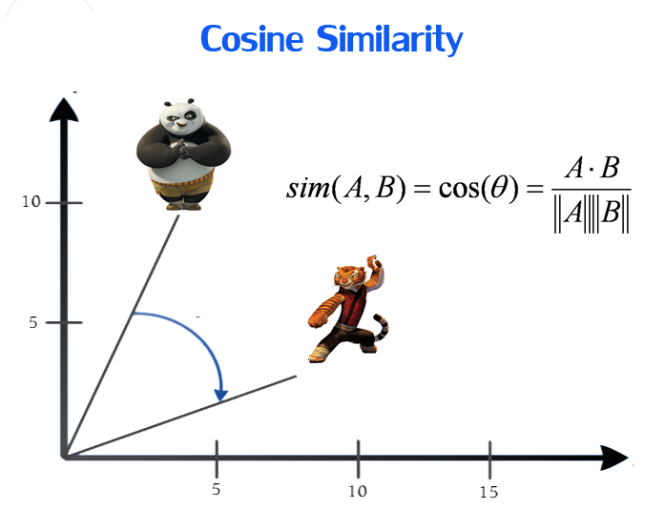
Introduction:

Matrix factorization is a very popular approach for solving a recommendation system. Basically, it is vector space model, which means that the model contains 2 major components:

Item representations ( an MxK matrix where M is the number of items and K is the number of latent dimension) and User representations (an NxK matrix where N is the number of users and K is the number of latent dimension).

There are 2 main application for a recommendation system in E-commerce:

Given a specific user, we would like to recommend relevant items based on their past behavior. (for the time being, we’ll simply call this application “Items to user” recommendation)
Given a specific item, we would like to find similar items to the desire one. (we’ll simply call this one “Items to Item” recommendation)

(For a detail explanation of vector space model, please refer to:

https://erikbern.com/2015/09/24/nearest-neighbor-methods-vector-models-part-1.html)

In this paper, we don’t want to delve into the detail of matrix factorization engine, instead we’re trying to solve a problem when deploying a recommendation system into production.

Problem definition:

For “Items to Items” recommendation, given an item, we’ll have to calculate the similarity score for the entire remain items (we often used cosine similarity for scoring which range from -1 to 1, where more similar items tend to have score close to 1). This is often called exhaustive search, which means that we must scan through all the document (items in our case) to get the similarity score.

For small-size document, a naive approach of exhaustive search may do fine in a reasonable time. However, in real life situation, the size of document may often scale up to hundred thousands or millions of items, in which case an exhaustive search over all document would be both computationally expensive and time-consuming.

This problem also happen when we want to get recommendations for a specific user. In this case, to get relevant items for a user, we would scan all the items available to compute the “rating” using inner product between user vector and item vector(this term is only accurate when we use explicit matrix factorization, however if we do implicit matrix factorization, we could simply replace this term with “score”). Again, this procedure incurs a lot of computation expense on our system.

Solution

So the idea is that, instead of searching all over the search space, we’ll come up with a strategy that search only a small portion of the search space. In this case, we used LSH (Locality sensitive Hashing), an approach that enable us to search for approximate nearest neighbors for a given point in metric space. This approach have proved to be more efficient than KD-tree , especially when the dimension of the search space is high (>100).

(For a detail explanation of LSH, please refer to:

https://erikbern.com/2015/10/01/nearest-neighbors-and-vector-models-part-2-how-to-search-in-high-dimensional-spaces.html)

There are a lot of implementation of LSH out there in Python, to name a few: nmslib, annoy, faiss, … These are considered the fastest library for LSH in terms of speed. In this paper, we’ll make use of Annoy for nearest neighbors search because of its popularity, speed, and ease of use compared to other library. (nmslib is a prominent library, but I haven’t yet tried it

In the case of “Items to item” recommendation, implementing LSH into our engine is very straightforward: just input the item representations matrix (you don’t have to normalize it before hand) into the model and let it do the job.

One thing worth noting is that: the distance metric this time is “angular distance”, which basically is the Euclidean distance between 2 points in metrics space (where their corresponding vectors have been normalized). To get a deeper understanding of why this is the case, please take a look at explanation:

Enough said, let’s program this thing up:

The training phase often take a few minute to complete.

For “Items to user” recommendation, the solution is not easy. To know why it is the case, please read this paper: https://arxiv.org/pdf/1202.6101v1.pdf

Basically, this paper show that we can’t implement the LSH to “Items to user” with inner-product similarity metric. Luckily, there is a paper publish by Microsoft that show a beautiful transformation which can reduce the “Maximum inner product search” to “Nearest neighbor search with Euclidean distance”, therefore this transformation allow us to directly apply LSH to our recommendation problem. This transformation could be summarized in a theorem which formalized by researchers at Microsoft:

Simply put, there are 2 steps in transformation:

+) First step happen during pre-processing stage: For each of item vector, we add an extra dimension so that all item vector have equal length (or norm L2 in mathematical term).

With this transformation during pre-processing stage, we’re able to reduce maximum inner-product search to nearest neighbor search in Euclidean distance. (Very smart, Microsoft researchers!)

+) The second step happen during query time: As mention above, we added one more dimension to the item vector, hence user vector have one less dimension than item vector.

So naturally, we would add an extra component to the user vector for the matrix multiplication to happen. But, what component should we add? Well it is 0, as stated in theorem 1 above.

This also assure that the inner product of the two new vectors would be the same as the inner product of the original ones (before transformation).

(https://www.microsoft.com/en-us/research/wpcontent/uploads/2016/02/XboxInnerProduct.pdf)

For those who just want to get to the result quickly, here is the full code adapt from this paper:

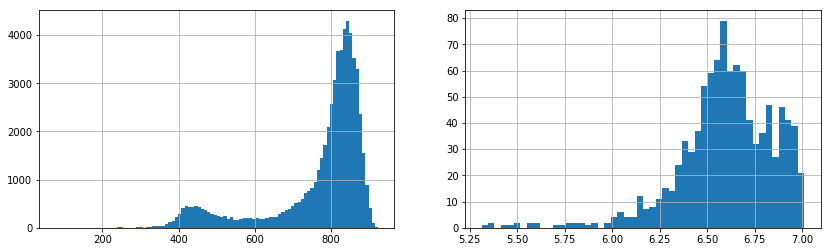
Compare performance between ANN search and Bruteforce search, the x-axis show the number of queries per second:

On the left graph: ANN and right graph: Bruteforce. We could see ANN approach outperform Bruteforce approach by 50–100 times.

Useful link:

https://github.com/benfred/implicit/issues/29

Annoy blog post:

Please follow and like us:

Using Approximate Nearest Neighbor for faster retrieval on Recommendation system

Introduction:

Problem definition:

Solution

Leave a Reply Cancel reply